请教Python中多组数据点拟合的问题，如何实现？
大约有 2000 个数据点，plot 出来基本是这样的。
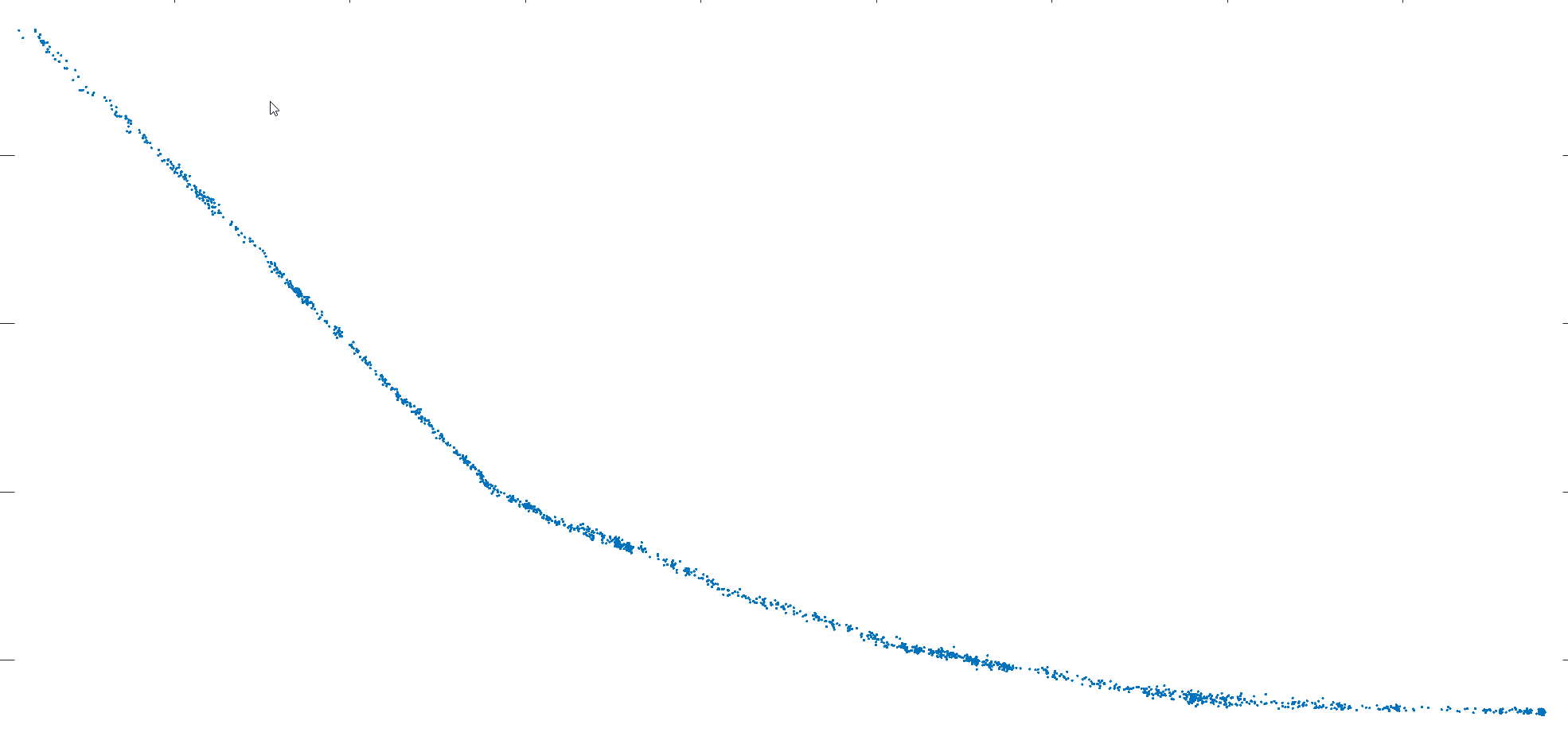
需要写一个脚本，实现的功能是：输入所有点的横纵坐标，然后进行分段一次线性拟合（需要分成 9 段，也就是需要确定 10 个点的坐标），使得最终整体的残差值最小，想用 Python 实现。
最终的结果示意如图。
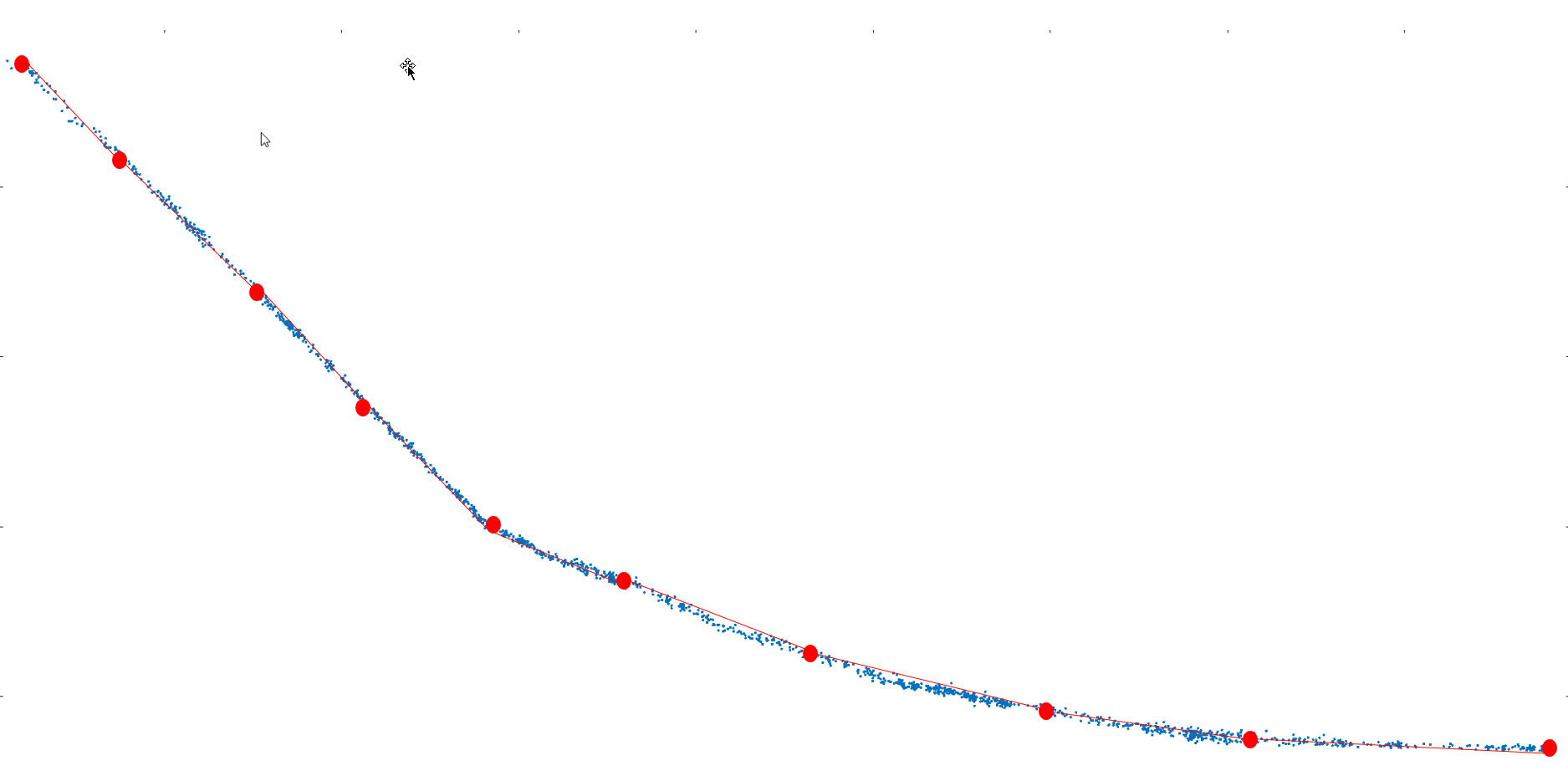
我之前使用 MATLAB 实现了，但是由于这个功能是整个项目的一部分，项目的整体是在用 Python，因此希望用 Python 实现。
之前的使用 MATLAB 实现的办法是：
- 使用 cftool 中的高斯拟合将 2000 个点拟合成 8 阶高斯曲线；
- 对拟合的曲线求二阶导数，然后找极值，极值绝对值较大的地方就是“弯曲”厉害的地方。从大到小排序，然后取包括前后端点在内的极值点的前十个，将十个点放在这些极值点的地方。 当然，实际写起来有些边界条件需要处理，这里就不详述了。
这个方法不是很优雅，而且效果不是很好。问题来了，Python 有没有更好的解决类似问题的办法？
提前感谢各位。
请教Python中多组数据点拟合的问题，如何实现？
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
# 定义要拟合的函数形式，例如二次函数
def func(x, a, b, c):
return a * x**2 + b * x + c
# 生成示例数据（多组）
x_data = [
np.array([1, 2, 3, 4, 5]),
np.array([1.5, 2.5, 3.5, 4.5, 5.5]),
np.array([0.5, 1.5, 2.5, 3.5, 4.5])
]
y_data = [
np.array([2.1, 3.9, 8.2, 15.1, 24.0]),
np.array([3.2, 5.1, 9.3, 16.0, 25.2]),
np.array([1.0, 2.8, 6.1, 12.0, 19.8])
]
# 合并多组数据
x_all = np.concatenate(x_data)
y_all = np.concatenate(y_data)
# 执行拟合
popt, pcov = curve_fit(func, x_all, y_all)
print(f"拟合参数: a={popt[0]:.3f}, b={popt[1]:.3f}, c={popt[2]:.3f}")
# 可视化
plt.figure(figsize=(10, 6))
x_fit = np.linspace(0, 6, 100)
y_fit = func(x_fit, *popt)
colors = ['red', 'blue', 'green']
for i, (x, y) in enumerate(zip(x_data, y_data)):
plt.scatter(x, y, color=colors[i], label=f'数据集 {i+1}', alpha=0.7)
plt.plot(x_fit, y_fit, 'k-', label=f'拟合曲线: y={popt[0]:.3f}x²+{popt[1]:.3f}x+{popt[2]:.3f}')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
核心就三步：1）定义函数模型；2）合并所有数据点；3）用curve_fit一次拟合。如果各组数据权重不同，可以通过sigma参数调整。
用合并数据的方法最直接。
对 numpy 不熟悉，以我朴素的数学知识瞎 bibi 下，
先锁定第一点 A 和最后一点 B，
然后假定加入中间的 i 点，变成 2 条线了，计算对应的方差 Di，确定第 3 个点 C=i, where Di= min D
再继续加入第 4 个点。。。。直到需要的点数，
2000 个数据点算起来应该也还好，最大问题可能是如果不巧的话，前面的点不好，后面的未必是最优的
#11 这的确是个好思路，我找到了[这个]( https://zh.wikipedia.org/zh-hans/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D%E6%B3%95)算法，还需要进一步想想。
#11 链接乱了，可能是 MD 语法少了空格。再贴一次 [这个]( https://zh.wikipedia.org/zh-hans/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D%E6%B3%95)
